- 4학년 안홍준 씨, MRI 왜곡 현상 개선 기법 개발 -
- 국제뇌기능매핑학회 공식 저널 〈NeuroImage〉게재 -
[연구필요성]
최근에는 고전컴퓨터로 시뮬레이션 하기 힘든 규모까지 양자컴퓨터가 발전해 있다. 다만 양자컴퓨터는 고전컴퓨터에 비해 본질적으로 오류에 취약한 성질 때문에 오류정정이 필요한데 아직까지 대규모 오류정정은 구현되어 있지 않다. 연구자들은 이러한 양자컴퓨터를 NISQ (Noisy Intermediate Scale Quantum)라고 칭하고 NISQ 시대에도 양자컴퓨터의 응용 가능성을 확인하기 위해 탐색 중에 있다. 그중에서 특히 양자컴퓨터와 고전컴퓨터를 동시에 이용하는 하이브리드방식이 많이 연구되어 왔지만 그 응용 영역이 제한되어 왔다.
[연구성과/기대효과]
연구성과: 기존에 이론적으로 제시된 하이브리드 알고리즘을 현재 오류가 있는 양자컴퓨터에서도 구현이 가능함을 보임으로 오류정정 이전의 양자컴퓨터의 응용 가능성을 확인했다.
기대효과 : 기존 다체계 물리에서 해결되지 않은 양자상 구분이나 바닥상태의 물리적 특징을 예측하는데 오류정정 이전의 양자컴퓨터도 도움을 줄 수 있다.
[본문]
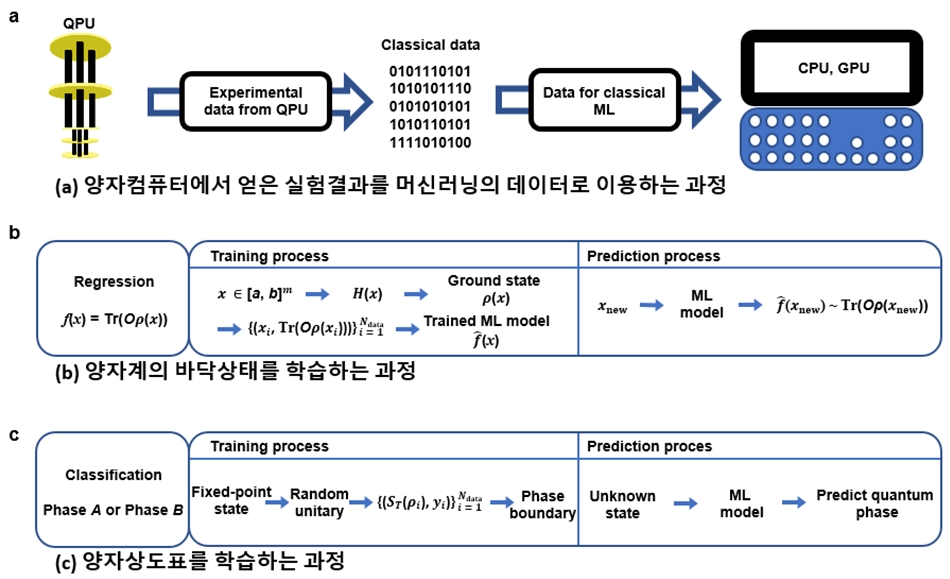
고전컴퓨터가 양자컴퓨터를 시뮬레이션하기 힘들지만 양자컴퓨터를 통해 데이터를 제공받으면 기존에 고전컴퓨터만을 이용하는 것보다 더 많은 문제를 풀 수 있다는 것이 연구되었다. 이에 대한 구체적인 응용 예시로 다체계 물리에서 중요한 문제인 바닥상태의 특성을 예측하는 것과 서로 다른 양자상을 구별할 수 있다는 것이 제안되었다.
위의 이론적인 제안에도 불구하고 아직 양자컴퓨터에서 발생하는 오류 때문에 실험적인 구현이 되어 있지 않았는데 본 연구에서 다양한 오류완화 기법을 결합 및 개발해서 현재의 오류가 있는 양자컴퓨터에서도 이론적으로 제시된 알고리즘을 구현할 수 있음을 보였다.
본 연구에서는 random hopping model이라는 양자 시스템의 바닥상태 특징을 학습하는 것이 가능함을 실험적으로 보였다. 이를 통해 양자컴퓨터에서 충분한 데이터를 제공한다면 이후에는 고전컴퓨터를 통한 학습을 통해 시스템의 바닥상태의 특징을 높은 정확도로 예측할 수 있음을 보였다. 구체적으로 학습된 모델을 통해 다체계 물리에서 위상학적 특징이 있다고 알려진 SSH (Su–Schrieffer–Heeger) model의 바닥상태의 특성을 높은 정확도로 예측했다.
서로 다른 양자상을 구분하는 것은 다체계 물리에서 많이 연구되어 왔다. 본 연구에서는 symmetry protected topological phase가 있는 양자 상태를 구분하는 것과 topologically ordered phase가 있는 양자상을 구분하는 문제를 수십 큐빗 규모에서 성공적으로 수행함으로 고전컴퓨터와 양자컴퓨터를 하이브리드로 이용하는 방식의 확장성을 확인했다.
[연구결과]
Machine learning on quantum experimental data toward solving quantum many-body problems
Gyungmin Cho, Dohun Kim
(Nature Communications 15, 7552 (2024), https://www.nature.com/articles/s41467-024-51932-3)
양자 컴퓨터는 과학 전 분야에 걸쳐 고전 컴퓨터로 접근이 어려운 특정 문제를 효율적으로 해결할 수 있는 잠재력을 가지고 있지만, 아직까지 완벽한 오류 정정법이 구현되지 않아 현재 하드웨어 기술수준 (Noisy Intermediate-Scale Quantum: NISQ 수준)으로 응용 가능한 양자 알고리즘의 종류가 제한되어 왔다. 양자컴퓨터의 활용성을 높이기 위한 방법으로 고전컴퓨터와 오류가 있는 양자컴퓨터를 동시에 이용하는 하이브리드 방식이 최근 제안되고 있다. 본 연구에서는 대부분 이론/시뮬레이션으로만 제안된 이 접근법을 실제 클라우드 양자컴퓨터를 사용하여 응용성을 크게 확장하는 연구를 수행하였다.
본 연구에서 개발한 하이브리드 접근 방식을 다체계 물리에서 중요한 두 가지 문제에 적용하였는데, 첫번째는 양자계의 바닥 상태 (많은 경우 계의 성질, 측정 기대값을 결정함)의 특성을 예측하는 것과 다양한 양자 상도표의 경계 (양자 효과에 의해 구별되는 상)을 식별하는 것이다. 본 연구에서는 기존연구와 차별적으로 다양한 오류 완화 기법 (오류 정정과 달리 특정 오류를 데이터의 후처리를 통해 소거하는 방법)을 적용하여 양자컴퓨터에서 정제된 데이터를 얻을 수 있었고 이를 이용해 기존에 이론적으로만 제시된 하이브리드 방식이 적용 가능성과 유용성이 높음을 실험적으로 검증하였다.
- 1.오류정정: 오류가 있는 물리 비트 여러 개를 모아 오류를 줄인 로직 비트를 만들어서 현재의 고전컴퓨터에 준하는 안정성을 구현하는 방법이다.
- 2.오류완화: 오류정정과 달리 특정 오류만을 상쇄시킬 수 있지만 비교적 적은 추가 자원으로 구현할 수 있다.
- 3.바닥상태: 주어진 시스템에서 가장 낮은 에너지를 갖는 상태로서 시스템이 평형상태에 있을 때 시스템의 성질을 결정함.
- 4.양자상: 양자효과에 의해 구별되는 서로 다른 상.
- 5.NISQ: Noisy Intermediate-Scale Quantum의 줄임말로 오류정정 이전의 양자컴퓨터이지만 고전컴퓨터로는 시뮬레이션하기 힘든 큐빗수를 (1000개 큐빗) 가진 양자컴퓨터를 이르는 말.
- 6.Random hopping model: 입자들이 랜덤하게 정해진 비율을 통해 주변 격자로 이동하는 시스템.
- 7.SSH (Su–Schrieffer–Heeger) model: 1차원에서 위상학적 특성이 나타나는 물리 현상을 설명하는 모형.
- 8.Symmetry protected topological phase: 특정 대칭이 유지될 때만 안정적으로 존재하는 물질의 상태
- 9.Topologically ordered phase: 여러 입자가 얽힌 상태로 존재해 준입자의 분수 전하나 비국소적 성질을 나타내는 새로운 물질 상태
[그림설명]